第21章 - 熵与热力学第三定律

I. 宏观熵

回顾一下，熵 $S$ 是一个描述无序度的状态函数。这意味着两个状态之间的熵变与路径无关，仅取决于起点和终点。到目前为止，我们将宏观熵变 $\Delta S$ 表示为可逆热流除以温度的积分：

$$\begin{equation*} \Delta S=\int \frac{\delta q_{r e v}}{T} \quad \leftrightarrow \quad d S=\frac{\delta q_{r e v}}{T} \tag{1} \end{equation*}$$

我们可以使用这个表达式和热力学第一定律，来推导其他用热容表示的 $\Delta S$ 的有用表达式：

对于恒容（等容）过程：

$$\begin{equation*} \Delta S=\int_{T_{1}}^{T_{2}} \frac{n \bar{C}_{V}(T)}{T} d T \tag{2} \end{equation*}$$

为了推导这个公式，我们从 $\Delta S=\int \frac{\delta q_{\text {rev }}}{T}$ 和第一定律：$d U=\delta q+\delta w$ 开始。由于 $\delta w=-P_{\text {ext }} d V$ 且在恒容条件下 $d V=0$，所以不做功，我们的表达式简化为 $d U=\delta q$。我们也知道 $d U=C_{V}(T) d T$ （或 $d U=n \bar{C}_{V}(T) d T$，其中 $\bar{C}_{V}(T)$ 是摩尔热容），这使得我们可以将恒容下的部分热流写为 $q_{V}=C_{V}(T) d T=n \bar{C}_{V}(T) d T$。使用我们的宏观熵表达式，恒容下的 $\Delta S$ 变为：

$$\Delta S=\int \frac{\delta q_{V}}{T}=\int \frac{d U}{T}=\int_{T_{1}}^{T_{2}} \frac{n \bar{C}_{V}(T)}{T} d T$$

对于恒压（等压）过程：

$$\begin{equation*} \Delta S=\int_{T_{1}}^{T_{2}} \frac{n \bar{C}_{P}(T)}{T} d T \tag{3} \end{equation*}$$

类似地，对于恒压过程，我们有 $\delta q_{P}=n \bar{C}_{P}(T) d T$。$\Delta S$ 变为：

$$\Delta S=\int \frac{\delta q_{P}}{T}=\int_{T_{1}}^{T_{2}} \frac{n \bar{C}_{P}(T)}{T} d T$$

III. 绝对熵与热力学第三定律

到目前为止，我们一直关注系统的熵变 $\Delta S$。使用方程3并令 $T_{1}=0$，我们可以写出绝对熵的表达式：

$$\begin{equation*} S\left(T_{2}\right)=S(0 K)+\Delta S ; \quad \text { 例如 } S\left(T_{2}\right)=S(0 K)+\int_{0}^{T_{2}} \frac{C_{P}(T)}{T} d T \tag{12} \end{equation*}$$

我们可以将绝对熵看作是将物质从 0 K 开始，将所有使物质达到 $T_{2}$ 的相关过程（升温、相变）的 $\Delta S$ 加和起来。定义了绝对熵之后，我们就可以定义热力学第三定律了。

热力学第三定律指出，一个系统的熵 $S$ 是有限的正值，并且一个完美晶体物质在 0 K 时的熵为 0。这是合理的：一个完美晶体系统只有一种排列方式，所以 $S=k_{B} \ln W=k_{B} \ln (1)=0$。此外，对数函数永远不会是负数，因此根据定义 $S=k_{B} \ln W$，熵必须总是正值或零（在完美晶体的情况下）。

我们规定系统必须是“一个完美晶体物质”，是因为有些系统在 0 K 时存在一些熵，例如玻璃、一氧化碳以及包含不同晶体排列的系统。实际上，非晶体系统的绝对熵仍然非常小。因此，我们仍然可以近似认为：

$$\begin{equation*} S(0 K)=0 \tag{13} \end{equation*}$$

相变的熵

与焓类似，熵可以通过相变在给定温度下增加。

$$\begin{equation*} \Delta_{t r s} S=\frac{q_{r e v}}{T_{t r s}} \tag{14} \end{equation*}$$

相变是可逆过程的一个很好的例子。这是因为温度的任何微小变化都会引起相变的发生。

$$\begin{equation*} \Delta_{t r s} H=q_{P} \tag{15} \end{equation*}$$

因此，相变的熵与该相变的焓相关。

$$\begin{equation*} \Delta_{t r s} S=\frac{\Delta_{t r s} H}{T_{t r s}} \tag{16} \end{equation*}$$

熵是一个状态函数。为了计算一种物质在任意温度下的绝对熵，我们必须将升温和相变引起的熵变相加。对于一种气体：

$$\begin{equation*} \Delta S(T)=\int_{0}^{T_{\text {fus }}} \frac{C_{P}(T)}{T} d T+\frac{\Delta_{\text {fus }} H}{T_{\text {fus }}}+\int_{T_{\text {fus }}}^{T_{\text {vap }}} \frac{C_{P}(T)}{T} d T+\frac{\Delta_{\text {vap }} H}{T_{\text {vap }}}+\int_{T_{\text {vap }}}^{T_{1}} \frac{C_{P}(T)}{T} d T \tag{17} \end{equation*}$$

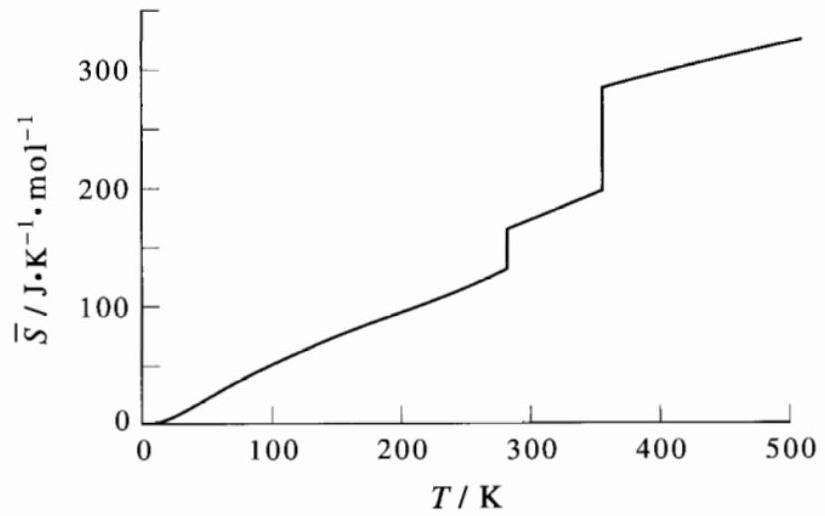
图 21.1 氮的摩尔熵随温度（从 0 K 到 400 K）变化的曲线图。

与焓类似，我们可以使用标准摩尔熵来计算一个反应的熵变。对于以下通式反应，

$$\begin{equation*} a A+b B \rightarrow y Y+z Z \tag{18} \end{equation*}$$

该反应的熵变为：

$$\begin{equation*} \Delta_{r} S^{\circ}=y S^{\circ}[Y]+z S^{\circ}[Z]-a S^{\circ}[A]-b S^{\circ}[B] \tag{19} \end{equation*}$$

最后，有一些普遍趋势需要记住：

• 气体的标准摩尔熵大于固体。
• 质量增加会增加热无序度，因此标准摩尔熵也增加。
• 分子越大，标准摩尔熵越大。
• 越“松软”的分子（柔性分子）具有越大的标准摩尔熵。
• 储存在分子间作用力中的能量越多，标准摩尔熵越大。”